鉄筋コンクリート造梁付着の断面検定
記号説明
<鉄筋コンクリート構造計算規準・解説 1991>
$b$ :長方形梁の幅(mm)
$D$ :梁せい(mm)
$d_t$上 :鉄筋重心位置(上端引張)(mm)
$d_t$下 :鉄筋重心位置(下端引張)(mm)
$j$上 :応力中心間距離(上端引張)(mm)
$j$下 :応力中心間距離(下端引張)(mm)
$f_aL$ :長期許容付着応力度(N/mm2)
$f_aS$ :長期許容付着応力度(N/mm2)
$τ_a$ :設計用せん断応力度(N/mm2)
$σ_t$ :引張鉄筋継手部分の応力度(フックを設ける場合には2/3倍した値、N/mm2)
$l_d$ :付着検定断面からの付着長さ(mm)
必要長 :必要延長長さ
<鉄筋コンクリート構造計算規準・解説 1999>
$b$ :長方形梁の幅(mm)
$D$ :梁せい(mm)
d上 :有効せい(上端引張)(mm)
d下 :有効せい(下端引張)(mm)
$σ_t$ :引張鉄筋継手部分の応力度(フックを設ける場合には2/3倍した値、N/mm2)
$l_d$ :付着検定断面からの付着長さ(mm)
$l_{db}$ :必要付着長さ
検討方法(鉄筋コンクリート構造計算規準・解説 1991)
・検定断面位置は左端、左端カットオフ位置、右端カットオフ位置、右端とします。
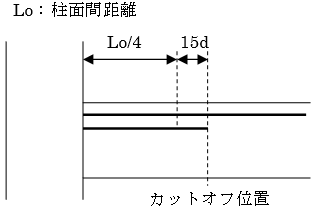
・カットオフ位置は柱面間距離の1/4から15d(指定により変更可能)中央側の位置とします。
・付着応力度の検定は以下の式により行います。
$τ_a=Q/φ_j≦f_a$
$Q$ :長期、短期荷重時の設計用せん断力
$j$ :曲げ材の応力中心間距離
$d$ :梁の有効せい
$φ$ :引張鉄筋の周長の総和
$f_a$ :許容付着応力度
・スパン途中の鉄筋端までの距離の検定は以下の式により行います。
$l_d≧σ_t・a/(0.8f_a・φ)+j$
$l_d$ :算定位置から鉄筋端までの長さ(通し筋では反対側の柱面までの長さ)
$a$ :鉄筋断面積
$φ$ :鉄筋周長
$f_a$ :許容付着応力度
$j$ :曲げ材の応力中心間距離
検討方法(鉄筋コンクリート構造計算規準・解説 1999)
・検定断面位置は左端、左端カットオフ位置、中央、右端カットオフ位置、右端とします。
・カットオフ位置は以下のように設定します。
1.端部鉄筋が中央鉄筋より多い場合、柱面間距離の1/4から15d中央側の位置とします。
2.中央鉄筋が端部鉄筋より多い場合、柱面間距離の1/4から20d端部側の位置とします。
・付着長さldは以下のように設定します。
| 左端 | 1/4位置 | 中央 | 3/4位置 | 右端 | |
|---|---|---|---|---|---|
| カットオフ無し | (通し筋長さ+d)/2 | 算定しない | 通し筋長さ/2 | 算定しない | (通し筋長さ+d)/2 |
| カットオフ有り (端部が多い場合) | CL | 残りが通し筋: (Lo-CL+d)/2 それ以外:Lo-CL-CR+d | 算定しない | 残りが通し筋:(Lo-CR+d)/2 それ以外:Lo-CL-CR+d | CR |
| カットオフ有り (中央が多い場合) | 算定しない | CL+d (Cは中央断面からの距離) | (Lo/2-CL),(Lo/2-CR) の小さい方 | CR+d (Cは中央断面からの距離) | 算定しない |
$L_o$ :柱面間距離
$C$ :カットオフ位置(添え字L,Rはそれぞれ左端・右端)
$d$ :有効せい
・必要付着長さldbは以下のように計算します。
$l_{db}=σ_t・A_s/(K・f_b・φ)$
$σ_t$ :付着検定断面位置における鉄筋引張応力度
フックを設ける場合には2/3倍とする
$A_s$ :当該鉄筋の断面積
$φ$ :当該鉄筋の周長
$f_b$ :許容付着応力度(1段筋以外は0.6を乗じる)
$K$ :鉄筋配置と横補強筋による以下の修正係数
(長期荷重時)$0.3・C/d_b+0.4$
(短期荷重時)$0.3・(C+W)/d_b+0.4$
$d_b$ :曲げ補強鉄筋径
ただし、2.5を超える場合2.5とする
$C$ :鉄筋間のあき、最小かぶり厚さの3倍、鉄筋径の5倍のいずれか小さい値
$W$ :付着割裂面を横切る横補強筋効果を表す換算長さ
鉄筋径の2.5倍を超える場合は鉄筋径の2.5倍
$A_{st}$ :当該鉄筋列の想定される付着割裂面を横切る1組の横補強筋全断面積
$N$ :当該鉄筋列の想定される付着割裂面における鉄筋本数
$s$ :1組の横補強筋($A_{st}$)の間隔
検討方法(鉄筋コンクリート構造計算規準・解説 2018)
- 検定断面位置は左端、左端カットオフ位置、中央、右端カットオフ位置、右端とします。
- 「上端1段」「上端2段」「下端2段」「下端1段」毎にカットオフタイプを決定し、検定断面位置に以下の表の条件に合致しない場合は検定しません。
- 引張り出ない場合は検定しません。
- カットオフ位置は以下のように設定します。
1.端部鉄筋が中央鉄筋より多い場合、柱面間距離の1/4から15d中央側の位置とします。
2.中央鉄筋が端部鉄筋より多い場合、柱面間距離の1/4から20d端部側の位置とします。
| カットオフタイプ | 左端 | 1/4位置 | 中央 | 3/4位置 | 右端 |
|---|---|---|---|---|---|
| カットオフ無し | (通し筋長さ+d)/2 | 算定しない | 通し筋長さ/2 | 算定しない | (通し筋長さ+d)/2 |
| カットオフ有り (端部が多い場合) | CL | 残りが通し筋: (Lo-CL+d)/2 それ以外:Lo-CL-CR+d | 算定しない | 残りが通し筋:(Lo-CR+d)/2 それ以外:Lo-CL-CR+d | CR |
| カットオフ有り (中央が多い場合) | 算定しない | CL+d (Cは中央断面からの距離) | (Lo/2-CL),(Lo/2-CR) の小さい方 | CR+d (Cは中央断面からの距離) | 算定しない |
長期荷重に対する使用性のための検討
長期荷重に対する使用性確保のための検討は、下式のいずれかを満たすかどうかを確認します。
$ \tau_{a1}=\cfrac{Q_L}{\Sigma \psi \cdot j} \leq _L f_a \left( \text{曲げ付着応力度} \right) $
$ \tau_{a2}=\cfrac{_L \sigma _t \cdot d_b}{4(l_d-d)} \leq 0.8 _L f_a \left( \text{平均付着応力度} \right) $
$Q_L$ :長期荷重時せん断力
$\psi$ :鉄筋の周長
$d$ :有効せい
$j$ :応力中心間距離($=7/8*d$)
$l_d$ :引張鉄筋の付着長さで、(16.2), (16.4), (16.6)式において、せん断ひび割れが生じない※ことが確かめられた場合、式中の$l_d-d$を$l_d$として計算します
$_L \sigma _t$ :検定断面位置における長期荷重時の鉄筋存在応力度で、鉄筋端に標準フックを設ける場合はその値の2/3とします
$_L f_a$ :長期許容付着応力度
※せん断ひび割れが生じるかどうかは、せん断応力が使用性確保のための長期許容せん断耐力(RC基準2018の(15.1)式)を上回るかどうかを判定します
短期荷重に対する損傷制御のための検討
短期荷重に対する損傷制御のための検討は、下式のいずれかを満たすかどうかを確認します。
$ \tau_{a1} = \cfrac{Q_L+Q_E}{\Sigma \phi \cdot j} \leq _S f_a … \left( \text{曲げ付着応力度} \right) $
$ \tau_{a2} = \cfrac{_S \sigma _t \cdot d_b}{4(l_d-d)} \leq 0.8 _S f_a … \left( \text{平均付着応力度} \right) $
$Q_E$:水平荷重時せん断力
$_S \sigma _t$:検定断面位置における短期荷重時の鉄筋存在応力度で、鉄筋端に標準フックを設ける場合はその値の2/3とします
$_S f_a$:短期許容付着応力度
大地震動に対する安全性確保のための検討
通し筋の場合
下式を満たすかどうかを確認します。 $ \tau_D=\alpha_1 \cdot \cfrac{\sigma_D \cdot d_b}{4(L'-d)} \leq K \cdot f_b$
$\alpha_1$:通し筋の応力状態を表す係数で、両端が曲げ降伏する部材を仮定して下表により求めます
| 両端が曲げ降伏する 部材の通し筋 | 1段目の鉄筋 | 2 |
| 多段配筋の2段目以降の鉄筋 | 1.5 | |
| 一単曲げ降伏で他端弾性の部材の通し筋 | 1 | |
$\sigma_D$:検定断面位置における安全性検討用の鉄筋引張応力度で、曲げ降伏する部材を仮定して$σ_y$とします
$σ_y$:検定断面位置における鉄筋の降伏強度で、鉄筋端に標準フックを設ける場合はその値の2/3とします
$L$:部材の内法長さ
$l’$:検定断面からカットオフ筋が計算上不要となる断面までの距離で、両端曲げ降伏部材を仮定して下式で求めます
$l’=\cfrac{A_{cut}}{A_{total}} \cdot \cfrac{L}{2}$
$A_{cut}$:カットオフされる引張鉄筋の断面積
$A_{total}$:カットオフされる引張鉄筋の断面積
$L’$:通し筋の付着長さで、検定断面にカットオフ筋がなく通し筋のみの場合は$L’=L$, 通し筋とカットオフ筋の両方がある場合は$L’=L-l’$とします
なお、(16.5)式において、部材にせん断ひび割れが生じないことが確かめられた場合、式中の$L’-d$を$L’$とします
$K$:鉄筋配置と横補強筋の修正係数(RC規準2018の(16.9)式によります)
$f_b$:付着割裂の基準となる強度で、下表によります
| 安全性確保のための検討 | ||
|---|---|---|
| 上端筋 | その他鉄筋 | |
| 普通コンクリート | $$0.8 \times \displaystyle \left( \frac{F_c}{40} + 0.9 \right)$$ | $$ \frac{F_c}{40} + 0.9 $$ |
| 軽量コンクリート | 普通コンクリートに対する値の0.8倍 | |
2. $F_c$はコンクリートの設計基準強度(N/mm2)を表す
3. 多段配筋の1段目(断面外側)以外の鉄筋に対しては、上表の値に0.6を乗じる
カットオフ筋の場合
下式を満たすかどうかを確認します。
$ \tau_D=\alpha_2 \cdot \cfrac{\sigma_D \cdot d_b}{4(l_d-d)} \leq K \cdot f_b$
ただし、$l_d \geq l’+d$
$\alpha_2$:カットオフ筋の応力状態を表す係数で下表により求めます
| 付着長さがL/2以下 のカットオフ筋 | 1段目の鉄筋 | 1 |
| 多段配筋の2段目以降の鉄筋 | 0.75 | |
| 付着長さがL/2を超えるカットオフ筋 | 1 | |