鉄骨鉄筋コンクリート造柱の断面検定
記号説明
$b$ :柱の幅(mm)
$D$ :柱のせい(mm)
$d_t$ :引張縁から引張鉄筋重心までの距離(mm)
$l$ :部材長、内法(mm)
位置 :断面算定位置(mm)
$_ra_t$ :引張鉄筋の断面積(mm2)
$β$ :鉄骨ウェブ材の形式と寸法による係数
$α’$ :$α、b’/b$によって決まる係数
$M_L$ :長期設計用曲げモーメント(kN・m)
$M_{sn}$ :積雪荷重による曲げモーメント(kN・m)
$M_{E1}$ :正加力時の地震荷重による曲げモーメント(kN・m)
$M_{E2}$ :負加力時の地震荷重による曲げモーメント(kN・m)
$M_{W1}$ :正加力時の風荷重による曲げモーメント(kN・m)
$M_{W2}$ :負加力時の風荷重による曲げモーメント(kN・m)
$M_{s1}$ :正加力時の短期設計用曲げモーメント(kN・m)
$M_{s2}$ :負加力時の短期設計用曲げモーメント(kN・m)
$_rM_A$$_L$ :鉄筋コンクリート部分の長期許容曲げモーメント(kN・m)
$_sM_A$$_L$ :鉄骨部分の長期許容曲げモーメント(kN・m)
$M_{AL}$ :長期許容曲げモーメント(=${s}M{AL}$+ $_rM _{AL}$)(kN・m)
$_rM _{AS}$ :鉄筋コンクリート部分の短期許容曲げモーメント(kN・m)
$_sM _{AS}$ :鉄骨部分の短期許容曲げモーメント(kN・m)
$M_{AS}$ :短期許容曲げモーメント(=$sM{AS}$+ $rM{AS}$)(kN・m)
$_rM_u$ :鉄筋コンクリート部分の終局曲げモーメント(kN・m)
$M_L/M_{AL}$ :長期曲げモーメントの検定値
$M_S/M_{AS}$ :短期曲げモーメントの検定値
$N_L$ :長期設計用圧縮力(kN)
$N_{sn}$ :積雪荷重による圧縮力(kN)
$N_{E1}$ :正加力時の地震荷重による圧縮力(kN)
$N_{E2}$ :負加力時の地震荷重による圧縮力(kN)
$N_{w1}$ :正加力時の風荷重による圧縮力(kN)
$N_{w2}$ :負加力時の風荷重による圧縮力(kN)
$N_{s1}$ :正加力時の短期設計用圧縮力(kN)
$N_{s2}$ :負加力時の短期設計用圧縮力(kN)
$_rN_L$ :鉄筋コンクリート部分の長期許容圧縮力(kN)
$_sN_L$ :鉄骨部分の長期許容圧縮力(kN)
$_rN_s$ :鉄筋コンクリート部分の短期許容圧縮力(kN)
$_sN_s$ :鉄骨部分の短期許容圧縮力(kN)
$Q_L$ :長期荷重によるせん断力(kN)
$Q_{sn}$ :積雪荷重によるせん断力(kN)
$Q_E$ :地震荷重によるせん断力(kN)
$Q_W$ :風荷重によるせん断力(kN)
$Q_s$ :短期設計用せん断力(kN)
$_sQ_D$ :鉄骨部分の短期設計用せん断力(kN)
$_rQ_D$ :鉄筋コンクリート部分の短期設計用せん断力(kN)
$Q_{AL}$ :長期許容せん断力(kN)
$_sQ _{AD}$ :鉄骨部分の短期許容せん断力(kN)
$_rQ _{AD}$ :鉄筋コンクリート部分の短期許容せん断力(kN)
軸力および曲げモーメントに対する検討
a) 軸力および曲げモーメントに対する検討
設計用軸力および曲げモーメントが許容耐力を下回ることを、以下の検定式により確認します1)。許容耐力については、鉄筋コンクリート部分と鉄骨部分の累加(累加強度式)により算定します。
■$_rN_t≦N≦_rN_c$または$M≧_sM_0$のとき
$N=_rN$
$M≦_sM_0+_rM$
■$N>_rN_cまたはM<_sM_0$のとき
$N=_rN_c+_sN$
$M=_sM$
■$N<_rN_c$または軸方向力が引張で$M<_sM_0$のとき
$N≧_rN_t+_sN$
$M≦_sM$
$N$:設計用圧縮力
$_rN_t$:鉄筋コンクリート部分が引張力のみを受ける場合の許容引張力
$_rN_c$:鉄筋コンクリート部分が圧縮力のみを受ける場合の許容圧縮力
$_rN$:鉄筋コンクリート部分の許容圧縮力
$M$:設計用曲げモーメント
$_rM$:鉄筋コンクリート部分の許容曲げモーメント
$_sM_0$:鉄骨部分が曲げモーメントのみ受ける場合の許容曲げモーメント
$_sM$:鉄骨部分の許容曲げモーメント
$_sN_c,_sN_t,_sM_0,_sN,_sM$は下式により算定します。
$_sN_c = _s A \cdot _s f_c$
$_sN_t = _s A_e \cdot _s f_t$
$_sM_o = _s Z \cdot _s f_t$
■$_sN$が圧縮力の場合
$\frac{_sN}{_sA} + \frac{_sM}{_sZ} = _s f_c$
■$_sN$が引張力の場合
$\frac{_sN}{_sA} + \frac{_sM}{_sZ} = _s f_t$
$_sA$:鉄骨部分の断面積
$_sA_e$:ボルト穴を控除した鉄骨部分の有効断面積(現在未考慮:sAe=sA)
$_sf_c$:鉄骨の許容圧縮応力度
$_sf_t$:鉄骨の許容引張応力度
$_sZ$:鉄骨の断面係数
1) 日本建築学会:鉄骨鉄筋コンクリート構造計算基準・同解説;P.11-14,86-97 1987.6
rNc,rNtは下式により算定します。
$_rN_c$ = min ($rN{c1}$, $rN{c2}$)
$_rN_c$$_1$ = $A_e \cdot f_c'$
$_rN_c$$_2$ = $\frac{A_e \cdot _m f_c’}{n}$
$_rN_t = - _m A \cdot _m f_t$
$A_e$:コンクリートの等価断面積
$_mA$:柱の全主筋断面積
$_mf_c$:主筋の許容圧縮応力度
$n$:ヤング係数比
$f_c$’:柱の鉄筋コンクリート部分の算定に用いるコンクリート許容圧縮応力度
$f_c’ = f_c \cdot (1-15 \cdot _s p_c)$
$f_c$:コンクリートの許容圧縮応力度
$_sp_c$:圧縮側鉄骨比(=$_sa_c/(b・D)$)
$_sa_c$:圧縮側鉄骨フランジの断面積
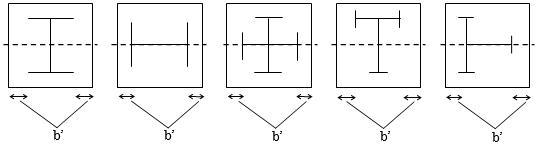
ここで、$f_{c’}$算定用の圧縮側鉄骨フランジ断面積($_sa_c$)のとり方の例を以下に示します。圧縮側鉄骨フランジとして、下図の太線で示す部分をとります。
$f_{c’}$算定用の圧縮側鉄骨フランジ断面積($_sa_c$)のとり方
$_rN,_rM$は以下により求めます。
■コンクリートで決まる場合
$0 < x_{n1} \verb|≦| 1$のとき
$_rn$ = $\frac{_rN}{b \cdot D \cdot f_c’}$ = $\frac{x_n1}{2} + n \cdot _mp_t \cdot \left( 2- \frac{1}{x_n1} \right)$
$_rm = \frac{_rM}{b \cdot D^2 \cdot f_c’} = \frac{x_n1}{12} \cdot (3-2 \cdot x_n1) + \frac{n \cdot _m p_t}{2 \cdot x_n1} \cdot (1-2 \cdot _{r}d_t1)^2$
$0 < x_{n1} \verb|≦| 1$のとき
$_rn = \frac{_rN}{b \cdot D \cdot f_c’} = (1+2 \cdot n \cdot _m p_t) \cdot \left( 1- \frac{1}{2 \cdot x_n1} \right)$
$_rm = \frac{_rM}{b \cdot D^2 \cdot f_c’} = \frac{1}{2 \cdot x_n1} \cdot \left( \frac{1}{6} + n \cdot _m p_t \cdot (1-2 \cdot _{r}d_t1)^2 \right)$
■圧縮鉄筋で決まる場合
$\frac{_rN}{b \cdot D \cdot _mf_t} = \frac{x_n1}{ n \cdot (x_n1 - _rd_c1)} \cdot _rn$
$\frac{_rM}{b \cdot D^2 \cdot _mf_t} = \frac{x_n1}{ n \cdot (1-_rd_t1-x_n1)} \cdot _rm$
■引張鉄筋で決まる場合
$0 < x_{n1} \verb|≦| 1$のとき
$\frac{_rN}{b \cdot D \cdot _mf_t} = \frac{x_n1}{ n \cdot (1-_rd_t1-x_n1)} \cdot _rn$
$\frac{_rM}{b \cdot D^2 \cdot _mf_t} = \frac{x_n1}{ n \cdot (1-_rd_t1-x_n1)} \cdot _rm$
$x_{n1} < 0$のとき
$\frac{_rN}{b \cdot D \cdot _mf_t} = \frac{_mp_t \cdot (2 \cdot x_n1-1)}{1-_rd_t1-x_n1}$
$\frac{_rM}{b \cdot D^2 \cdot _mf_t} = \frac{_mp_t \cdot (1-2 \cdot _rd_t1)^2}{1-_rd_t1-x_n1}$
$x_{n1}$:柱の鉄筋コンクリート部分の中立軸比(=$x_n/D$)
$x_n$:曲げ材の圧縮縁から中立軸までの距離
$_rd_t$$_1$:rdtの全せいに対する比(=$_rd_t/D$)
$_rd_t$:引張縁から引張主筋重心までの距離
$_rd_c$$_1$:$_rd_c$の全せいに対する比(=$_rd_c/D$)
$_rd_c$:圧縮縁から圧縮主筋重心までの距離
$r_n$:鉄筋コンクリート部分の許容軸方向力の無次元化量
$r_m$:鉄筋コンクリート部分の許容曲げモーメントの無次元化量
$n$:ヤング係数比
$_mp_t$:引張鉄筋比
$_mf_t$:主筋の許容引張応力度
$f_c’$:柱の鉄筋コンクリート部分の算定に用いるコンクリートの許容圧縮応力度
せん断力に対する検討
設計用せん断力が許容せん断力を下回ることを、次式により確認します。
$Q \verb|≦| Q_A$ (長期せん断力の検定)
$_sQ_D$ $\verb|≦|$ $_sQ _{AD}$ および $_rQ_D$ $\verb|≦|$ $_rQ _{AD}$ (短期せん断力の検定)
a) 許容せん断力【SRC規準】
鉄骨および鉄筋コンクリート部分の許容せん断力はSRC規準により算定します1)。長期許容せん断力($_sQ_A$)は下式により求めます。
$Q_A$ = $(1+\beta) \cdot _rQ _{AL}$
$_rQ _{AL}$ = $b \cdot _rj \cdot a’ \cdot f_s$
$a’ = \left( \begin{array}{rr} _ra : \frac{b’}{b} \verb|≧| \frac{_ra}{3} \ 3 \frac{b’}{b} : \frac{b’}{b} < \frac{_ra}{3} \ \end{array} \right)$
1) 日本建築学会:鉄骨鉄筋コンクリート構造計算規準・同解説;96-97, 1987.6
$b$:柱幅
$_rj$:鉄筋コンクリート部分の圧縮側と引張側の応力中心間距離(=$7/8・_rd$)
$f_s$:コンクリートの許容せん断応力度
$ r_α $ : せん断スパン比による割増係数
$_ra $ = $ \frac{4}{_rM/(_r Q \cdot _r d)+1}$ かつ $1 \verb|≦| _{r}a \verb|≦| 2$
$_rM$:鉄筋コンクリート部分の設計用曲げモーメント
柱頭、柱脚の設計用曲げモーメントのうち大きい方とする。
$_rQ$:鉄筋コンクリート部分の設計用せん断力
柱頭、柱脚の設計用せん断力のうち大きい方とする。
$b’$:鉄骨フランジ位置でのコンクリート有効幅
β:鉄骨ウェブの形式と寸法による係数
$β = \left( \begin{array}{rr} \frac{n \cdot t_w \cdot _s d }{b \cdot _r j} \ \frac{1.33n \cdot b_f \cdot t_f }{b \cdot _r j} \ \end{array} \right)$
n:ヤング係数比
$t_w$:鉄骨のウェブ厚さ
$_sd$:鉄骨のフランジ重心間距離
$b_f$:鉄骨のフランジ幅
$t_f$:鉄骨のフランジ厚さ
鉄骨部分の短期許容せん断力は下式によります。
$_sQ_A = \left( \begin{array}{rr} d_w \cdot t_w \cdot _s f_s \ \frac{4}{3} \cdot b_f \cdot t_f \cdot _s f_s \ \end{array} \right)$
$d_w$:鉄骨ウェブ長さ(=H-2t2)
$_sd$:鉄骨のフランジ重心間距離
$_sf_s$:鉄骨の許容せん断応力度
鉄筋コンクリート部分の短期許容せん断力は下式によります。
$_rQ _{AS}$ = min ($_rQ _{A1}$, $_rQ _{A2}$)
$_rQ _{AS1}$ = $b \cdot _rj \cdot$ $(f_s+0.5 \cdot p_w \cdot _wf_t)$
$_rQ _{AS2}$ = $b \cdot _r j \cdot \left(2 \frac{b’}{b} \cdot f_s+p_w \cdot _wf_t \right)$
$p_w$: 帯筋比
$_wf_t$:主筋の許容圧縮応力度
b) 設計用せん断力
【構造規定】
SRC柱設計用せん断力決定方法を「構造規定」とした場合、鉄骨および鉄筋コンクリート部分の設計用せん断力は、構造規定により算定します2)。
■短期設計用せん断力
鉄骨部分の短期設計用せん断力($_sQ_D$)、鉄筋コンクリート部分の短期設計用せん断力($_rQ_D$)は次式により算定します。
$_sQ_D = \frac{_sZ}{_sZ+_ra_t \cdot _rj } \cdot Q_L+ \frac{_sM_1+_sM_2}{h’}$ (鉄骨部分)
$_rQ_D$= min ($_rQ _{D1}$,$_rQ _{D2}$) (鉄筋コンクリート部分)
$_sQ _{D1}$ = $\frac{_ra_t \cdot _rj}{_sZ+_ra_t \cdot _rj }Q_L+ \cdot Q_L+ \frac{_sM_1+_sM_2}{h’}$
$_sQ _{D2}$ = $n \cdot (Q_L+Q_E-_sQ_D)$
$_sM_1$:鉄骨部分の一端の短期許容曲げモーメント(N・mm)
$_sM_2$:鉄骨部分の他端の短期許容曲げモーメント(N・mm)
h’:柱の内法高さ(mm)
$_rM_1$:鉄筋コンクリート部分の一端の終局曲げモーメント(N・mm)
$rM_2$:鉄筋コンクリート部分の他端の終局曲げモーメント(N・mm)
n:割増係数
積雪時、暴風時においては、短期設計用せん断力算定式の$Q_L$を$Q_L+Q_S$$_n$、$Q_L+Q_W$に置き換えて求めます。
【SRC規準】
SRC柱設計用せん断力決定方法を「SRC規準」とした場合、鉄骨部分および鉄筋コンクリート部分の設計用せん断力は以下により算定します2)。
■短期設計用せん断力
鉄骨部分の短期設計用せん断力($_sQ_D$)、鉄筋コンクリート部分の短期設計用せん断力($_rQ_D$)は次式により算定します。
$_sQ_D = \frac{_sM_d}{M_s } (Q_L+Q_E)$ (鉄骨部分)
ここで、$_sM_d = _s M_o$、$_rM_d = M_s-_s M_d$
2) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.664-665,2007.8