鉄筋コンクリート接合部の終局耐力

鉄筋コンクリート造接合部の終局耐力

接合部検定表の符号一覧

鉄筋コンクリート造接合部の終局検定表の符号一覧を以下に示します。

 $κ$ ：接合部の形状による係数

  $κ=1.0$ 十字形接合部

  $κ=0.7$ ト形およびＴ形接合部

  $κ=0.4$ Ｌ形接合部

 $φ$ ：直交梁の有無による補正係数

  $φ=1.0$ 両側直交梁付き接合部

  $φ=0.85$ 上記外の場合

 $b_b$ ：梁幅（大きい方）

 $b_1$ ：梁面から平行する柱側までの距離（左）

 $b_2$ ：梁面から平行する柱側までの距離（右）

 $b_{a1}$ ：$\frac{b_1}{2}$または$\frac{D}{4}$の小さい方

 $b_{a2}$ ：$\frac{b_2}{2}$または$\frac{D}{4}$の小さい方

 $D_j$ ：下側柱せい

 $h_c$ ：上階階高

 $h_c$’ ：下階階高

 $T_u$ ：上端鉄筋引張力（スラブ筋^注1）含む）

 $T_u^{\prime}$ ：下端鉄筋引張力

 $M_{b}$：上端引張降伏モーメント

 $M_{b’}$ ：下端引張降伏モーメント

 $Q_{cu}$ ：上下柱の存在せん断力の平均

 $Q_{du}$：梁降伏時の鉄筋引張降伏力 - 柱せん断力

 $α$ ：接合部せん断力の割増率（$=1.0$）

 $V_{ju}$ ：形状から計算される終局せん断耐力

鉄筋コンクリート造接合部の終局耐力

終局検定においては、5章の非線形解析モデルによる荷重増分解析結果に対し、以降に示す靭性指針による終局耐力を用いて検定を行います。ここで、TおよびT’は計算条件の指定により、両端ヒンジ時応力もしくは存在応力から選択できます。

$$V_{ju} = \kappa \cdot \phi \cdot F_j \cdot b_j \cdot D_j$$

$$Q_{du} = a \cdot (T_u+T_u^{\prime}-Q_{cu})$$

$$V_{ju}/Q_{du}$$

柱によるせん断力

$ Q_{cu} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \frac{Q_{c1}+Q_{c2}}{2} & \displaystyle \left( \text{柱せん断力:存在応力の場合} \right)　\\ \displaystyle 2 \frac{M_b+M_b’}{h_c+h_c’} & \displaystyle \left( \text{柱せん断力:大梁両端ヒンジの場合} \right) \end{array} \right. \end{align}$

$Q_{c1}$:上側柱せん断力

$Q_{c2}$:下側柱せん断力

梁によるせん断力

正加力時：接合部の左側大梁を上引張、右側大梁を下引張
負加力時：接合部の左側大梁を下引張、右側大梁を上引張

上端引張側

$ T_{u} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \frac{M}{j_{tu}} & \displaystyle \left( \text{大梁せん断力:存在応力の場合} \right)　\\ \displaystyle \Sigma (\alpha_{up_i} \cdot a_{t_i} \cdot \sigma_{y_i} ) + \alpha_{up_{slab}} \cdot a_{t_{slab}} \cdot \sigma_{y_{slab}} & \displaystyle \left( \text{大梁せん断力:大梁両端ヒンジの場合} \right) \end{array} \right. \end{align}$

$j_{tu}$:上端鉄筋引張時の応力中心間距離

下端引張側

$ T_{u}^{\prime} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \frac{M}{j_{td}} & \displaystyle \left( \text{大梁せん断力:存在応力の場合} \right)　\\ \displaystyle \Sigma (\alpha_{up_i} \cdot a_{t_i} \cdot \sigma_{y_i} ) & \displaystyle \left( \text{大梁せん断力:大梁両端ヒンジの場合} \right) \end{array} \right. \end{align}$

$j_{td}$:下端鉄筋引張時の応力中心間距離

接合部降伏による強度低下率βj

現状、判定には使用してませんが、鉄筋コンクリート構造保有水平耐力計算規準・解説に記載の接合部降伏による強度低下率βjを計算した結果を「静的解析計算書」、「CSV出力」で出力します。

$\Sigma A_t$:柱梁接合部の左右大梁の引張主筋の断面積
   正加力時：接合部の左側大梁を上引張、右側大梁を下引張
   負加力時：接合部の左側大梁を下引張、右側大梁を上引張

$f_y$:大梁引張鉄筋の基準強度（$395N/mm^2$を超える場合は$395N/mm^2$となる）

$b_j$:柱梁接合部の有効幅（解説図20.19）

$D_b$:梁せい

$F_c$:接合部の基準強度
   柱梁接合部の入力が優先されます。指定がない場合は「下の柱のFc」、「上の柱のFc」の順番で認識します。

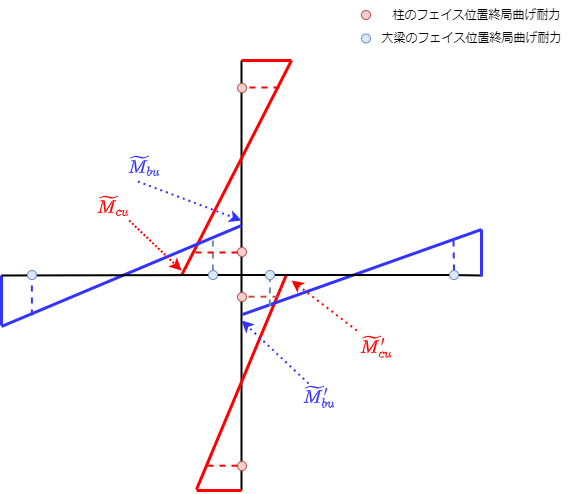
$\widetilde{M}_{cu}, \widetilde{M}^{\prime}_{cu}$:上下柱がフェイス位置で終局曲げ耐力となる場合の節点モーメント

$\widetilde{M}_{bu}, \widetilde{M}^{\prime}_{bu}$:左右大梁がフェイス位置で終局曲げ耐力となる場合の節点モーメント

   節点位置のモーメントはフェイス位置の終局耐力から計算します。
   接合部周辺部材の接合部に取りつかない方の耐力からの直線で結んだ値となります。

$\Sigma A_{iw}$:柱梁接合部内の横補強筋断面積総和
   取りつく梁の上端筋と下端筋の最少距離と柱幅に接合横補強筋比Pwを乗じた値となります。Pwは柱梁接合部の入力が優先されます。指定がない場合は終局検定条件2の入力が採用されます。

$f_{jy}$:柱梁接合部の横補強筋（$390N/mm^2$を超える場合は$390N/mm^2$となる）
   柱梁接合部の入力が優先されます。指定がない場合は「上下の柱の基準強度が小さい方」を採用します。

$\xi_{\gamma}$:柱梁接合部の有効アスペクト比による補正係数（解説表20.1による）