固有値解析

非減衰自由振動方程式

$$ [M]{\ddot{x}} + [S]{x} = 0 $$

ここで、
$[M]$：質量マトリクス

$[S]$：剛性マトリクス

${x}$：変位ベクトル

${\ddot{x}}$：加速度ベクトル

は次式のような固有周期問題となります。

$$ \lambda{V} = [M]^{-1} [S]{V} $$

このとき、$[M]^{-1} [S]$は一般に対称行列ではなく、ロッキングを考慮した場合、 $[M]$

も対角行列とならないことから、以下に示すような対称行列の固有値問題に置換えて解きます。

まず、 $[M]$をコレスキーの平方根により、２つの三角行列の積で表します。

$$ [M] = [T] \times [T]^T $$

ここで、$[T]$は下半分の三角行列です。式(3)を式(2)に代入し、左から $[T]^T$を乗ずると、

$$ \lambda [T]^T {V} = \left( [T]^{-1} [S] \left[T^{-1}\right]^T \right) [T]^T {V} $$

となります。従って、$([T]^{-1}[S][T^{-1}]^T)$ の固有値、固有ベクトルを求めれば、式(4)の固有値、固有ベクトルおよび固有周期Tは次のように求まります。

$\lambda = \lambda^* \\ \{V\} = \left[T^{-1}\right]^T\{V^*\} \\ T = 2\pi/\sqrt{\lambda}$

なお、$([T]^{-1}[S][T^{-1}]^T)$ の固有値解析は、振動自由度がに300以下の場合はヤコビ法により、300を超える場合はサブスペース法により計算されます。

式(1)に外乱として地震力を考慮すると

$[M]\ddot{x}+[S]x = -[M]\ddot{z}$ (6)

ここで、$\ddot{z}$：地震加速度

${x} = [V]{q}$とおき、左から$[V]$を乗ずれば、式(7)のようにモード分解することができます。

${\ddot{q}} + [A]{q} = {p}$ (7)

ここで、

$[A] = ([V]^T[M][V])^{-1}[V]^T[S][V]$

${p}$ = $-([V]^T[M][V])^{-1} \times [V]^T[M]{\ddot{z}}$ = $-{\ddot{z}} \times { \beta }$

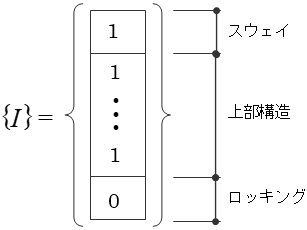
${\beta}$を刺激係数と呼び、ロッキング・スウェイを考慮した場合の式で表せば次のようになります。

${ \beta } = -([V]^T[M][V])^{-1}[V]^T[M]{I}$ (8)

ここで、